Distribuições Amostrais
ESTAT0078 – Inferência I
Prof. Dr. Sadraque E. F. Lucena
sadraquelucena@academico.ufs.br
http://sadraquelucena.github.io/inferencia1
- Cramér (1945):
- O objetivo fundamental da Teoria Estatística consiste em investigar a possibilidade de extrair dos dados inferências válidas.
Definição 2.1: Inferência Estatística
Seja \(X\) uma variável aleatória com função de densidade (ou de probabilidade) de parâmetro \(\theta\), denotada por \(f(x|\theta)\), e que não conhecemos o valor de \(\theta\) que representa a distribuição de \(X\).
Chamamos de inferência estatística o problema que consiste em especificar um ou mais valores para \(\theta\), com base em uma amostra de valores observados de \(X\).
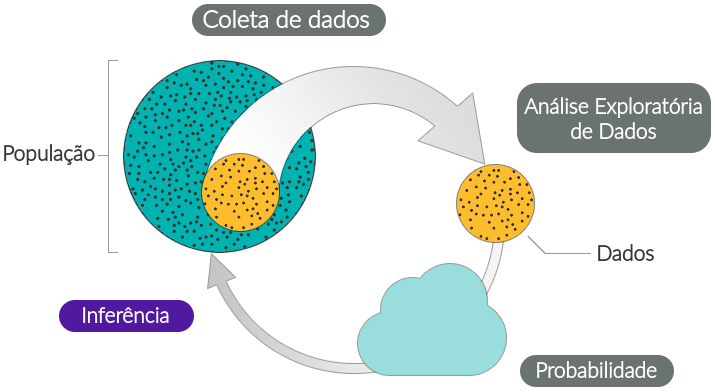
Tipos de problemas
- Problema de estimação: o objetivo é procurar, segundo algum critério especificado, valores que representem adequadamente os parâmetros desconhecidos.
- Exemplo: Estimar a idade média \(\mu\) da população de estudantes matriculados na UFS.
Tipos de problemas
- Teste de hipóteses: o objetivo é verificar a validade de afirmações sobre o valor de um ou mais parâmetros desconhecidos.
- Exemplo: Verificar se a proporção \(p\) de eleitores em determinada candidata é maior que 50% (ou 1/2) na população.
- Hipóteses: \(H_0 : p \leq 1/2\) contra \(H_1 : p > 1/2\).
- Exemplo: Verificar se o peso médio, \(\mu\), de pacotes de 1 kg empacotados por determinada máquina realmente é 1 kg.
- Hipóteses: \(H_0 : \mu = 1\) contra \(H_1 : \mu \neq 1\).
- Exemplo: Verificar se a proporção \(p\) de eleitores em determinada candidata é maior que 50% (ou 1/2) na população.
Definição 2.2: População
O conjunto de valores de uma característica observável associada a uma coleção de indivíduos ou objetos de interesse é dito ser uma população.
- A população é representada por uma variável aleatória \(X\) que descreve a característica de interesse.
Exemplos:
- Todas as transações de cartão de crédito realizadas em um país durante o ano de 2023.
- Todos os segurados de uma companhia de seguros de saúde.
Definição 2.3: Amostra
Qualquer parte (ou subconjunto) de uma população. A amostra é composta por \(n\) valores observados de uma característica de interesse, representados por variáveis aleatórias \(X_1, \ldots, X_n\). Ela é utilizada para fazer inferências sobre a população da qual foi retirada.
Exemplos:
Um conjunto de 1.000 transações de cartão de crédito realizadas em um país durante o ano de 2023.
Uma amostra de 500 segurados de uma companhia de seguros de saúde.
Definição 2.4: Parâmetro
Quantidade numérica que caracteriza uma determinada população.
- Em estatística, parâmetros são valores desconhecidos que descrevem as distribuições de variáveis aleatórias. Exemplos comuns de parâmetros incluem a média (\(\mu\)), a variância (\(\sigma^2\)) e a proporção (\(p\)).
Exemplo: Na distribuição normal \(N(\mu, \sigma^2)\), os parâmetros são
\(\mu\) (média)
\(\sigma^2\) (variância).
Definição 2.5: Espaço Paramétrico
Conjunto de todos os valores possíveis que os parâmetros de um modelo estatístico podem assumir.
- Ele define as restrições e o domínio dos parâmetros que são utilizados na modelagem de distribuições de probabilidades.
- Geralmente denota-se por \(\Theta\).
Exemplo: Para a distribuição \(N(\mu, \sigma^2)\), o espaço paramétrico é dado por \[ \Theta = \{(\mu,\sigma^2): -\infty<\mu<\infty, \sigma^2>0\}. \]
Definição 2.6: Estatística
Qualquer função \(\widehat{\theta} = T(X_1, \ldots,X_n)\) da amostra que não depende de parâmetros desconhecidos é denominada uma .
Exemplos:
- \(X_{(1)} = \min(X_1,\ldots,X_n)\)
- \(X_{(n)} = \max(X_1,\ldots,X_n)\)
- \(\widetilde{X} = \text{med}(X_1,\ldots,X_n)\)
- \(\overline{X} = \frac{1}{n}\sum\limits_{i=1}^n X_i\)
- \(\widehat{\sigma}^2 = \frac{1}{n} \sum\limits_{i=1}^n (X_i - \overline{X})^2\)
Definição 2.7: Estimador
Se \(\theta\) é um parâmetro de interesse e \(\Theta\) é o espaço paramétrico que define todos os valores possíveis que \(\theta\) pode assumir, então qualquer estatística que assuma valores dentro de \(\Theta\) pode ser considerada um estimador para o parâmetro \(\theta\).
Geralmente o estimador é denotado por uma letra grega com um chapéu (^) em cima, como em \(\hat{\theta}\).
A ideia por trás de um estimador é que ele fornece uma aproximação do valor verdadeiro do parâmetro com base nas observações da amostra.
Definição 2.7: Estimador
Exemplos:
Se \(\mu\) é a média de uma população, um estimador comum para \(\mu\) é a média amostral \(\hat{\mu} = \frac{1}{n} \sum_{i=1}^{n} X_i\).
Se \(\sigma^2\) é a variância de uma população, um estimador para \(\sigma^2\) é a variância amostral \(s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (X_i - \hat{\mu})^2\).
Definição 2.8
Qualquer estatística que assuma valores no conjunto dos possíveis valores de \(g(\theta)\) é um estimador para \(g(\theta)\).
Exemplo:
Considere que \(\theta\) seja a média de uma população, e queremos estimar uma função dessa média, especificamente \(g(\theta)=\theta^2\).
- Se \(\widehat{\theta}\) é o estimador da média \(\theta\), então o estimador para \(g(\theta)\) é dado por \[\widehat{g}(\theta) = g(\widehat{\theta}).\]
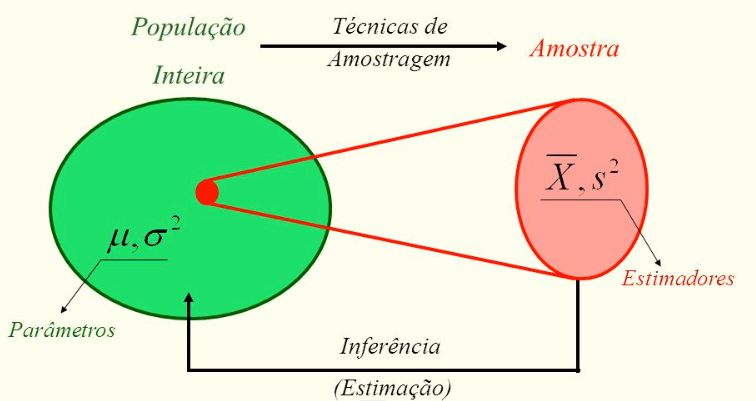
Fonte: https://slideplayer.com.br/slide/10934372/
Definição 2.9: Função de Verossimilhança
Uma amostra aleatória de tamanho \(n\) obtida de uma população \(X\) pode ser entendida como um conjunto de variáveis aleatórias, \(X_1, \ldots, X_n\), independentes e identicamente distribuídas com a mesma distribuição de \(X\).
- Se \(X\) tem uma distribuição com parâmetro \(\theta\), a função de densidade (ou função de probabilidade) conjunta de \(X_1,\ldots,X_n\) é chamada de e é dada por \[ L(\theta;\underset{\widetilde{\phantom{a}}}{x}) = f(x_1;\theta) f(x_2;\theta) \cdots f(x_n;\theta) = \prod_{i=1}^n f(x_i;\theta). \]
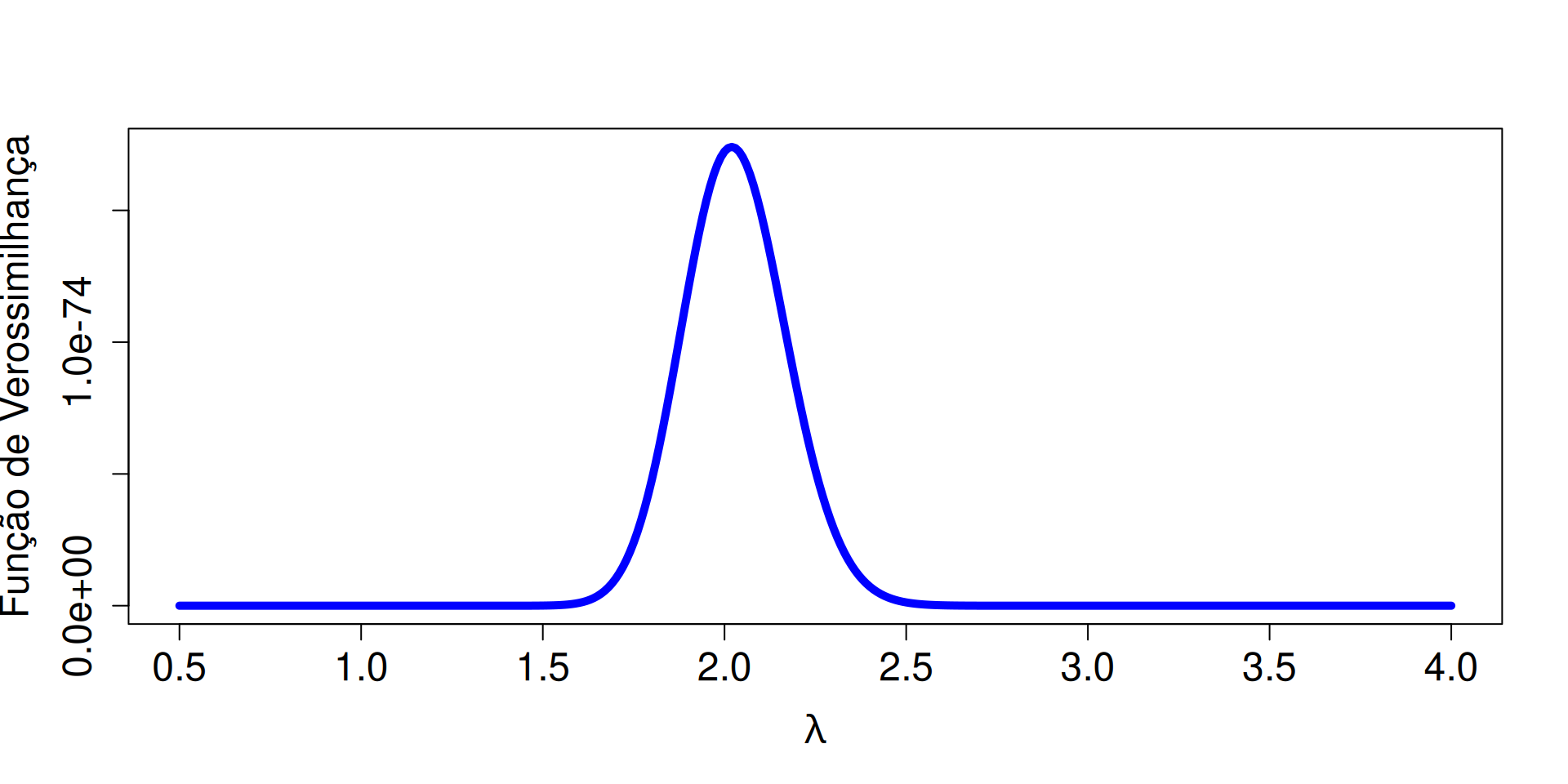
Exemplo 2.1
Suponha que estamos interessados no número de mortes por acidente de trânsito em um fim de semana comum, que pode ser modelado por uma variável aleatória \(X\) com distribuição de Poisson e parâmetro \(\lambda\). A função de probabilidade da Poisson(\(\lambda\)) é \[ f(x;\lambda) = \frac{e^{-\lambda}\lambda^x}{x!}, ~x = 0, 1, 2, \ldots \]
Agora, considere que temos uma amostra aleatória de tamanho \(n\), \(X_1,\ldots,X_n\), obtida dessa distribuição de Poisson. Encontre a função de verossimilhança, \(L(\lambda;\underset{\widetilde{\phantom{a}}}{x})\), dessa amostra aleatória.
Exemplo 2.1
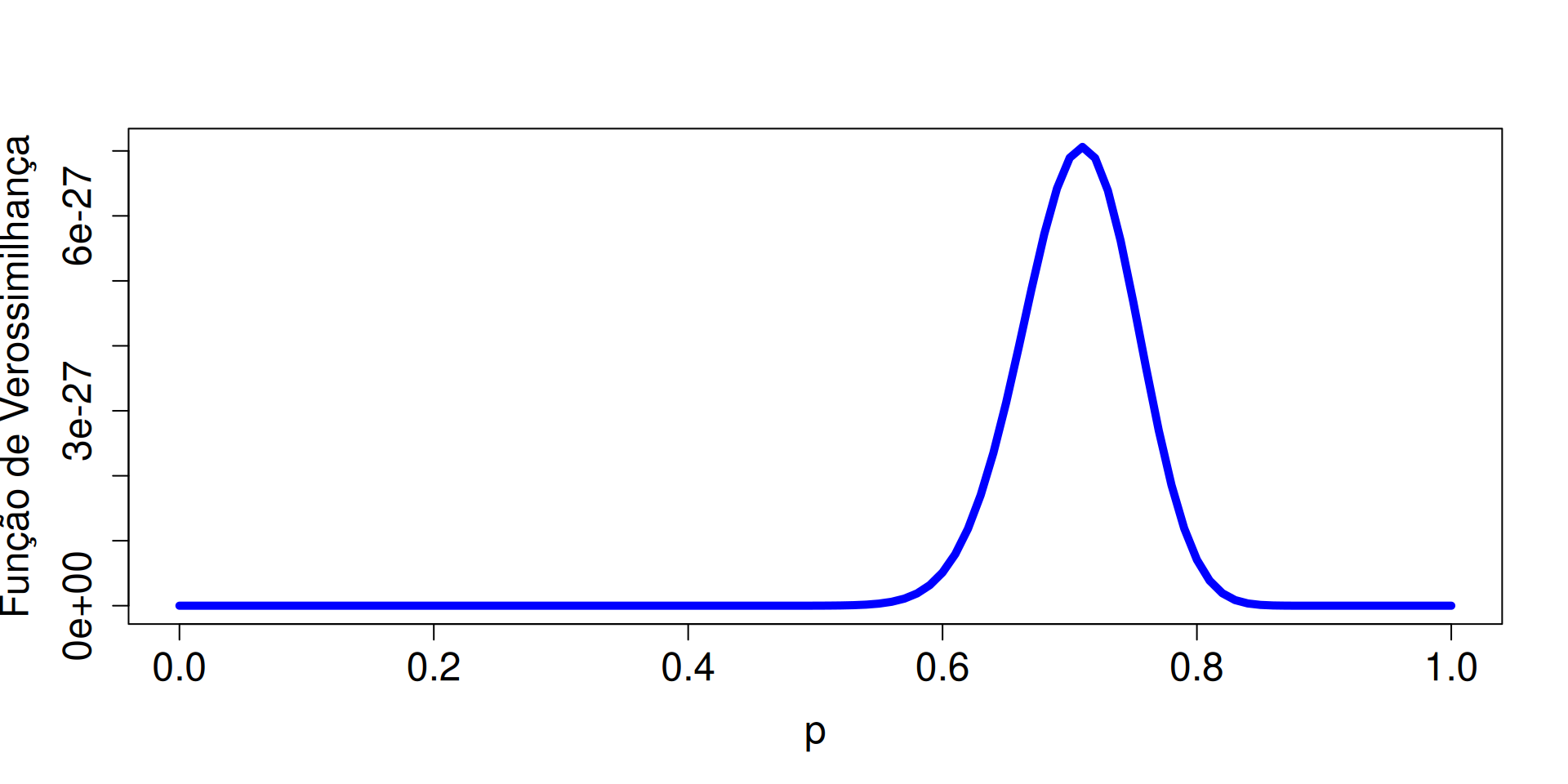
Exemplo 2.2
Imagine que uma empresa quer entender o cancelamento de assinaturas do seu serviço. A equipe de ciência de dados modela se um cliente cancela a assinatura como uma variável aleatória \(X\) com distribuição de Bernoulli de parâmetro \(p\), onde \(p\) é a probabilidade de um cliente manter a assinatura. A função de probabilidade da Bernoulli(\(p\)) é: \[ f(x;p) = p^x (1-p)^{1-x}, \quad x = 0, 1. \] Aqui, \(X=1\) indica que o cliente manteve a assinatura, e \(X=0\) indica que o cliente cancelou. Considere uma amostra aleatória de tamanho \(n\), \(X_1,\ldots,X_n\), obtida dessa distribuição de Bernoulli. Determine a função de verossimilhança, \(L(p;\underset{\widetilde{\phantom{a}}}{x})\), dessa amostra aleatória.
Exemplo 2.2
Exemplo 2.3
Pressuponha que o tempo de vida de um certo tipo de componente eletrônico, representado pela variável aleatória \(X\), tem distribuição Exponencial com parâmetro \(\alpha\). A função de densidade da Exponencial(\(\alpha\)) é: \[ f(x;\alpha) = \alpha e^{-\alpha x}, \quad x\geq 0. \]
Admita que uma amostra aleatória de tamanho \(n\), \(X_1,\ldots,X_n\), foi obtida dessa distribuição Exponencial. Determine a função de verossimilhança, \(L(p;\underset{\widetilde{\phantom{a}}}{x})\), para essa amostra aleatória.
Exemplo 2.3
Fim
