Viés de um Estimador
ESTAT0078 – Inferência I
Em inferência estatística, desejamos, a partir de uma amostra, obter conclusões sobre a população.
Mais especificamente, desejamos estimar um parâmetro \(\theta\) que desconhecemos a partir de um estimador \(\widehat{\theta}\), que é uma função da amostra.
Dada uma população, existem muitas e muitas amostras aleatórias simples (a.a.s) de tamanho \(n\) que podem ser sorteadas.
Cada uma dessas amostras pode resultar em um valor diferente da estatística de interesse (\(\overline{X}\) e \(S^2\), por exemplo).
Vejamos um exemplo.
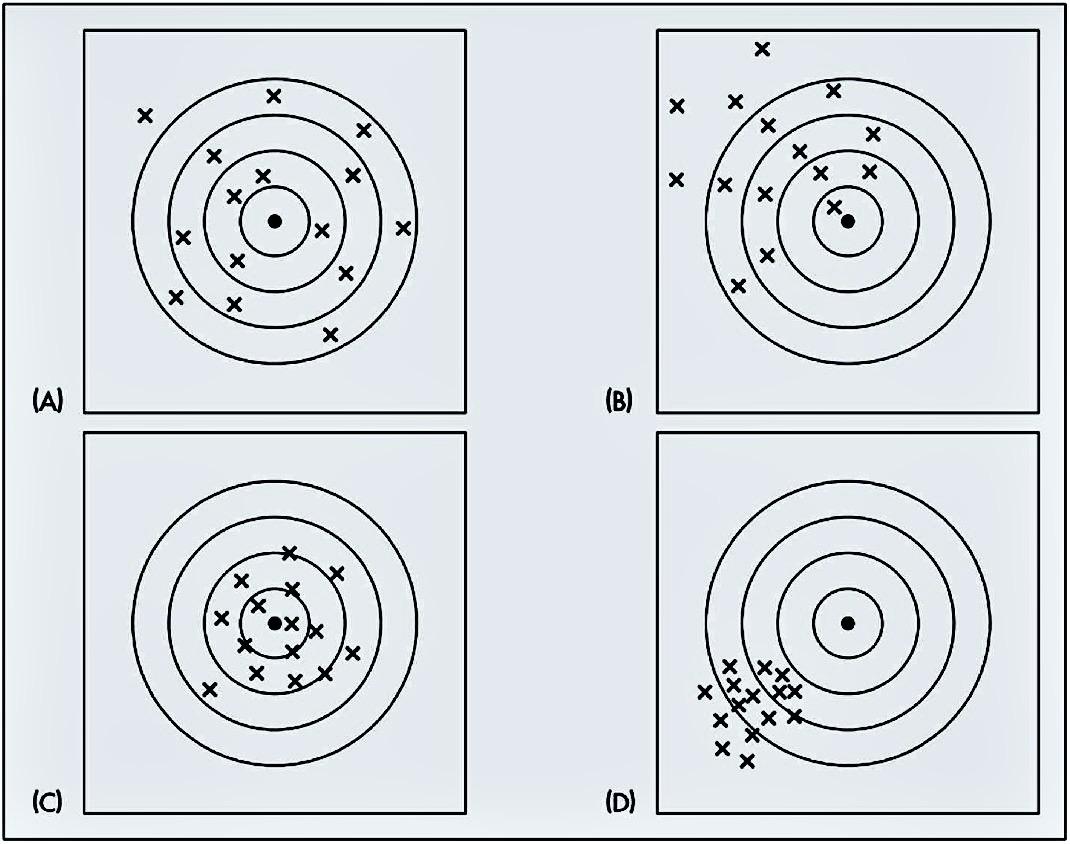
- O alvo representa o valor do parâmetro e os “tiros” representam os diferentes valores amostrais da estatística de interesse.
- (A\(\,\!\)) e (C) fornecem valores distribuídos em torno do verdadeiro valor do parâmetro, embora em (A) os valores estejam mais dispersos.
- Em (B) e (D) as estimativas estão centradas em torno de um valor diferente do parâmetro de interesse e na parte (D), a dispersão é maior.
- O nosso interesse então é obter estimadores que forneçam estimativas centradas em torno do verdadeiro valor do parâmetro.
- Queremos também que a dispersão das estimativas seja a menor possível.
- Essas duas propriedades estão associadas à esperança e à variância do estimador, que são medidas de centro e dispersão, respectivamente.
- Vejamos o conceito de viés de um estimador.
Definição 3.1: Viés de um estimador
O viés (ou vício) de um estimador \[
B(\widehat{\theta}) = E[\widehat{\theta}] - \theta.
\]
Dizemos que um estimador \(\widehat{\theta}\) é para \(\theta\) se \[
E[\widehat{\theta}] = \theta
\] para todo \(\theta\in\Theta\).
Note que se \(\widehat{\theta}\) é não viesado, \(B(\widehat{\theta})=0\).
Revisão: Esperança Matemática
Se \(X\) é uma v.a. discreta e \(Y\) é uma v.a. contínua, a esperança é dada por \[
E(X) = \sum_{i} x_i P(X=x_i) \quad \text{e} \quad E(Y) = \int\limits_{-\infty}^{\infty} y f(y) \, dy.
\] Para variáveis aleatórias \(X\) e \(Y\) e constantes \(a\) e \(b\):
\(E(a+bX) = a + b E(X)\)
\(E(X+Y) = E(X) + E(Y)\)
Se \(X\) e \(Y\) forem independentes, \(E(XY) = E(X)E(Y)\).
Essas propriedades valem para mais de duas variáveis aleatórias.
Revisão: Variância
\[
\begin{aligned}
Var(X) &= E[(X-E(X))^2] = E(X^2) - [E(X)]^2.
\end{aligned}
\]
Para variáveis aleatórias \(X\) e \(Y\) e constantes \(a\) e \(b\):
- \(Var(bX) = b^2 Var(X)\)
- Se \(X\) e \(Y\) são independentes, \[Var(X+Y) = Var(X)+Var(Y)\]
Essas propriedades valem para mais de duas variáveis aleatórias.
Exemplo 3.1
Seja \(X_1, X_2, \ldots, X_n\) uma amostra aleatória independente e identicamente distribuída de uma população com \(E(X)=\mu\) e \(Var(X)=\sigma^2>0\).
- \(\overline{X}\) é viesado para \(\mu\)?
- \(\widehat{\sigma}^2 = \frac{1}{n} \sum\limits_{i=1}^n (X_i-\overline{X})^2 = \frac{\sum\limits_{i=1}^{n} X_i^2 - n\overline{X}^2}{n}\) é viesado para \(\sigma^2\)?
- \(S^2 = \frac{1}{n-1} \sum\limits_{i=1}^n (X_i-\overline{X})^2 = \frac{\sum\limits_{i=1}^{n} X_i^2 - n\overline{X}^2}{n-1}\) é viesado para \(\sigma^2\)?
Definição 3.2: Estimador Assintoticamente Não Viesado
Seja \(\widehat{\theta}\) um estimador de um parâmetro desconhecido \(\theta\). Diz-se que \(\widehat{\theta}\) é um estimador assintoticamente não viesado de \(\theta\) se \[
\lim_{n\rightarrow\infty} E(\widehat{\theta}) = \theta,
\] ou, de forma equivalente, \[
\lim_{n\rightarrow\infty} B(\widehat{\theta}) = \lim_{n\rightarrow\infty} \left[ E(\widehat{\theta}) - \theta \right] = 0.
\]
Exemplo 3.2
Seja \(X_1, X_2, \ldots, X_n\) uma amostra aleatória independente e identicamente distribuída de uma população com \(E(X)=\mu\) e \(Var(X)=\sigma^2>0\).
- \(\overline{X}\) é assintoticamente não viesado para \(\mu\)?
- \(\widehat{\sigma}^2\) é assintoticamente viesado para \(\sigma^2\)?
- \(S^2\) é assintoticamente viesado para \(\sigma^2\)?
