Regressão Linear

ESTAT0109 – Mineração de Dados em Estatística

Prof. Dr. Sadraque E. F. Lucena
sadraquelucena@academico.ufs.br
http://sadraquelucena.github.io/mineracao

Objetivo da Aula

Distinguir Inferência de Predição e aplicar a Regressão Linear para modelar e prever uma variável contínua.

Panorama Geral de Mineração de Dados

Anteriormente exploramos o mundo Não Supervisionado:

Objetivo: Encontrar estrutura escondida nos dados (Ex: K-means).
Chave: Não tínhamos uma variável-resposta (Y).

Agora entraremos no mundo Supervisionado:

Objetivo: Prever um valor-alvo (Y) com base em outras variáveis (X).
A Grande Divisão:
1. Regressão: O Y é um número contínuo.
  - *Exemplo:** Prever a nota do IDEB, o valor do aluguel, a mortalidade infantil.
2. Classificação: O Y é uma categoria/rótulo.
  - Exemplo: Prever se um paciente tem COVID, se uma transação é fraude, se um aluno vai evadir o curso.

Problema: Aluguel de Bicicletas

Vamos usar a Regressão Linear para entender e prever o número de aluguéis de bicicleta (rentals) com base em condições climáticas.

Variável resposta (Y): rentals (numérica → Regressão)
Variáveis Preditoras (X): temperature, humidity, windspeed.

# Pacotes
library(tidyverse)
library(tidymodels) # Para dividir dados e métricas
library(patchwork) # Para juntar gráficos

# Carregando os dados
bikes <- read_csv("/home/sadraque/Documentos/UFS/Disciplinas/2025.2/mineracao de dados em estatistica/slides/08-regressao_linear/08-regressao_linear_exemplos/bikes.csv", col_types = "Dffffddddd")

Regra de Ouro da Aprendizagem Supervisionada

Nunca avalie seu modelo com os mesmos dados que você usou para treiná-lo.

Overfitting (Superajuste): Ocorre quando o modelo “decora” os dados de treino, mas não sabe generalizar para dados novos.
Analogia: É como um aluno que tira 10 na lista de exercícios (que ele decorou), mas tira 0 na prova (dados novos).
Queremos um modelo que vá bem na prova, não que apenas decore a lista.

Solução: Partição Treino-Teste

Vamos dividir nossos dados aleatoriamente:

Dados de Treino (~80%): A “lista de exercícios”. Usaremos para construir e inferir o modelo.
Dados de Teste (~20%): A “prova surpresa”. Ficarão guardados e só serão usados uma única vez, no final, para avaliar a capacidade de predição do modelo.

Solução: Partição Treino-Teste

# Fixando a semente para reprodutibilidade
set.seed(123) 

# Criando a partição com 'tidymodels'
# Usamos 'strata = rentals' para garantir que a distribuição de 'rentals' 
# seja similar nos dois conjuntos (importante!)
bikes_split <- initial_split(bikes, prop = 0.80, strata = rentals)

# Extraindo os dataframes de treino e teste
bikes_treino <- training(bikes_split)
bikes_teste  <- testing(bikes_split)

# Verificando os tamanhos
dim(bikes_treino)

[1] 583  10

dim(bikes_teste)

[1] 148  10

A Abordagem de “Dois Mundos”

A regressão linear pode ser usada para responder duas perguntas distintas:

Mundo 1: INFERÊNCIA (O Estatístico Clássico)

Pergunta: Quais variáveis explicam os aluguéis?
Ferramentas: lm(), summary(), p-valores, \(R^2\), Análise de Resíduos.
Dados: bikes_treino

Mundo 2: PREDIÇÃO (O Cientista de Dados/ML)

Pergunta: Quão bem meu modelo prevê aluguéis em dias novos?
Ferramentas: predict(), RMSE, MAE.
Dados: bikes_teste

Mundo 1: INFERÊNCIA (Explorando as Relações)

Primeiro, vamos explorar a correlação apenas nos dados de treino.

# Seus gráficos originais, agora aplicados aos dados de TREINO
p1 <- ggplot(bikes_treino, aes(x = temperature, y = rentals)) +
  geom_point(color = "#22562a", size = 2, alpha = .5) +
  theme_minimal(base_size = 14) +
  labs(title = "Temperatura vs. Aluguéis")

p2 <- ggplot(bikes_treino, aes(x = humidity, y = rentals)) +
  geom_point(color = "#27276d", size = 2, alpha = .5) +
  theme_minimal(base_size = 14) +
  labs(title = "Umidade vs. Aluguéis")

p3 <- ggplot(bikes_treino, aes(x = windspeed, y = rentals)) +
  geom_point(color = "#741012", size = 2, alpha = .5) +
  theme_minimal(base_size = 14) +
  labs(title = "Vento vs. Aluguéis")

(p1 + p2) / p3

Mundo 1: INFERÊNCIA (Explorando as Relações)

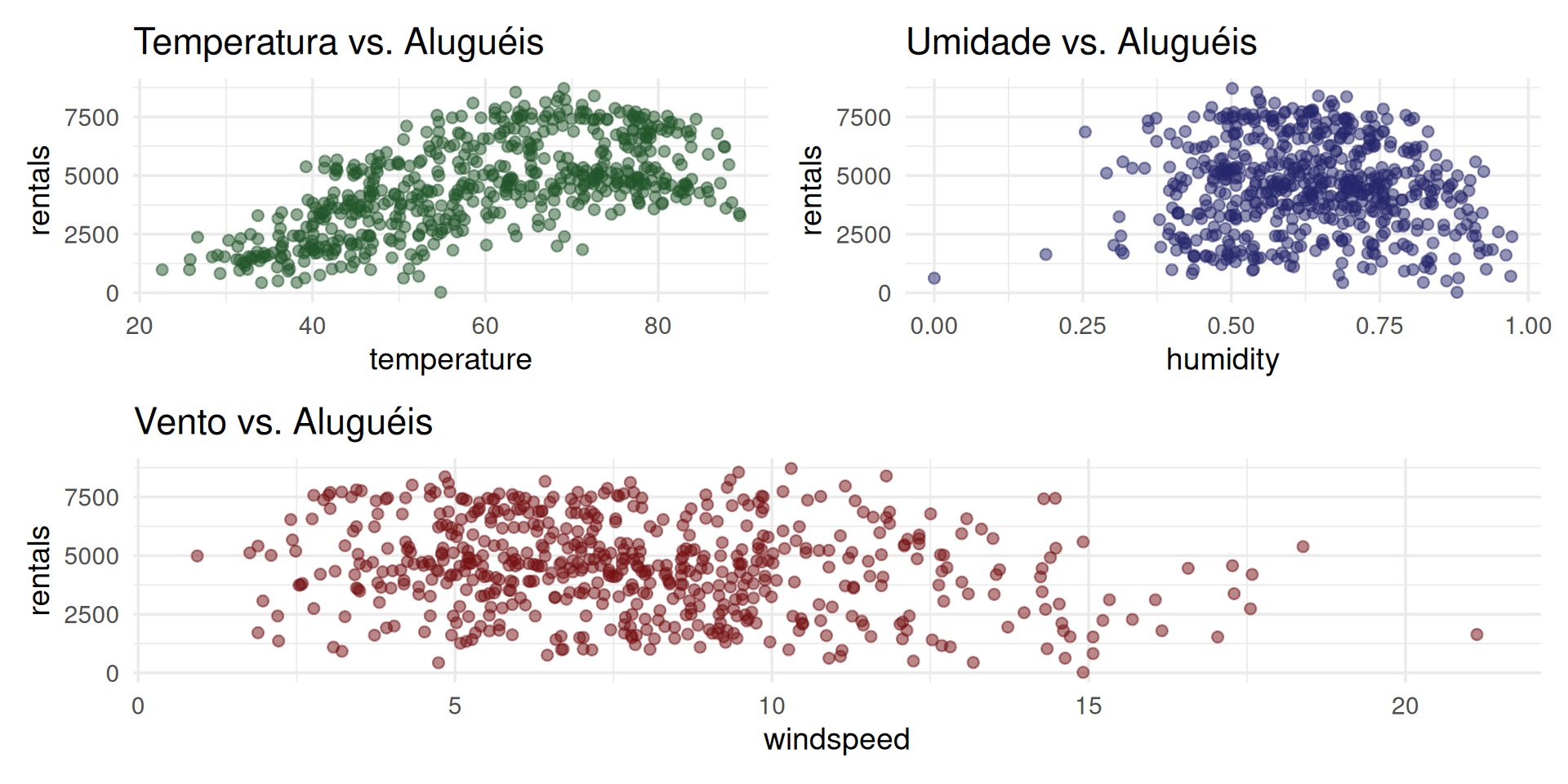
Insight: O gráfico Vento vs. Aluguéis mostra uma nuvem de pontos aparentemente aleatória. Se olhássemos só para ele, diríamos que windspeed (vento) não tem relação com rentals (aluguéis).

Mundo 1: Ajustando o Modelo Linear Múltiplo

Vamos ajustar nosso primeiro modelo de regresão linear múltipla usando a função lm() nos dados de treino.

\[ rentals = \beta_0 + \beta_1 temperature + \beta_2 humidity + \beta_3 windspeed + \varepsilon \]

# Ajustando o modelo v1
modelo <- lm(rentals ~ temperature + humidity + windspeed, 
                data = bikes_treino)

O summary() é a principal ferramenta de inferência.

summary(modelo) # Mostrando o sumário

Mundo 1: Interpretando o `summary()`


Call:
lm(formula = rentals ~ temperature + humidity + windspeed, data = bikes_treino)

Residuals:
    Min      1Q  Median      3Q     Max 
-4545.5 -1108.7  -103.4  1076.1  3649.7 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept)  2212.748    416.264   5.316 1.52e-07 ***
temperature    79.092      3.975  19.898  < 2e-16 ***
humidity    -2626.091    433.640  -6.056 2.51e-09 ***
windspeed     -95.367     19.655  -4.852 1.57e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 1450 on 579 degrees of freedom
Multiple R-squared:  0.4406,    Adjusted R-squared:  0.4377 
F-statistic:   152 on 3 and 579 DF,  p-value: < 2.2e-16

Mundo 1: Interpretando o `summary()`

Teste F (p-valor global): < 2.2e-16. O modelo como um todo é significativo (é melhor que um “chute” na média).
Testes t (p-valores individuais):
- temperature: Significativo (p-valor < 0.0001)
- humidity: Significativo (p-valor < 0.0001)
- windspeed: Significativo (p-valor < 0.0001)
- Se houvesse variáveis não significativas, deveríamos removê-las do modelo e rodar novamente.
Métricas de Ajuste:
- \(R^2\) Ajustado: 0.4377. Cerca de 43.77% da variabilidade dos aluguéis nos dados de treino é explicada pelo modelo.

Mundo 1: Interpretando o `summary()`

Insight: Este é um exemplo clássico de variável de confusão ou supressão. Sozinho, o vento não parece importar. Mas depois de controlarmos o efeito da temperature e humidity, o efeito real do vento aparece: com temperatura e umidade constantes, ventos mais fortes diminuem os aluguéis (coeficiente de -95.4). Isso mostra por que a Regressão Múltipla é mais poderosa que correlações simples.

Mundo 1: Diagnóstico (Validando as Suposições)

Para confiarmos nas nossas inferências (p-valores e intervalos de confiança), precisamos checar as suposições do modelo (análise de resíduos).

Observamos os gráficos:

**Resíduos vs. Valores Ajustados (Linearidade/Homocedasticidade):* A linha deve estar perto de zero e os pontos devem estar aleatórios.
Q-Q Plot (Normalidade dos Resíduos): Os pontos devem seguir a linha.
Scale-Location: Similar ao 1 (variância deve parecer constante).
Resíduos vs. Alavancagem (Pontos Influentes): Nenhuma Distância de Cook > 0.5 (sem pontos de grande influência).

Mundo 1: Diagnóstico (Validando as Suposições)

# Gráficos de diagnóstico do R base
par(mfrow = c(2, 2), bg = "#F5F5F5", mar = c(4, 4, 2, 1))
plot(modelo, pch = 20, col = "#27276d", cex = 1.5)

par(mfrow = c(1, 1)) # Resetar layout

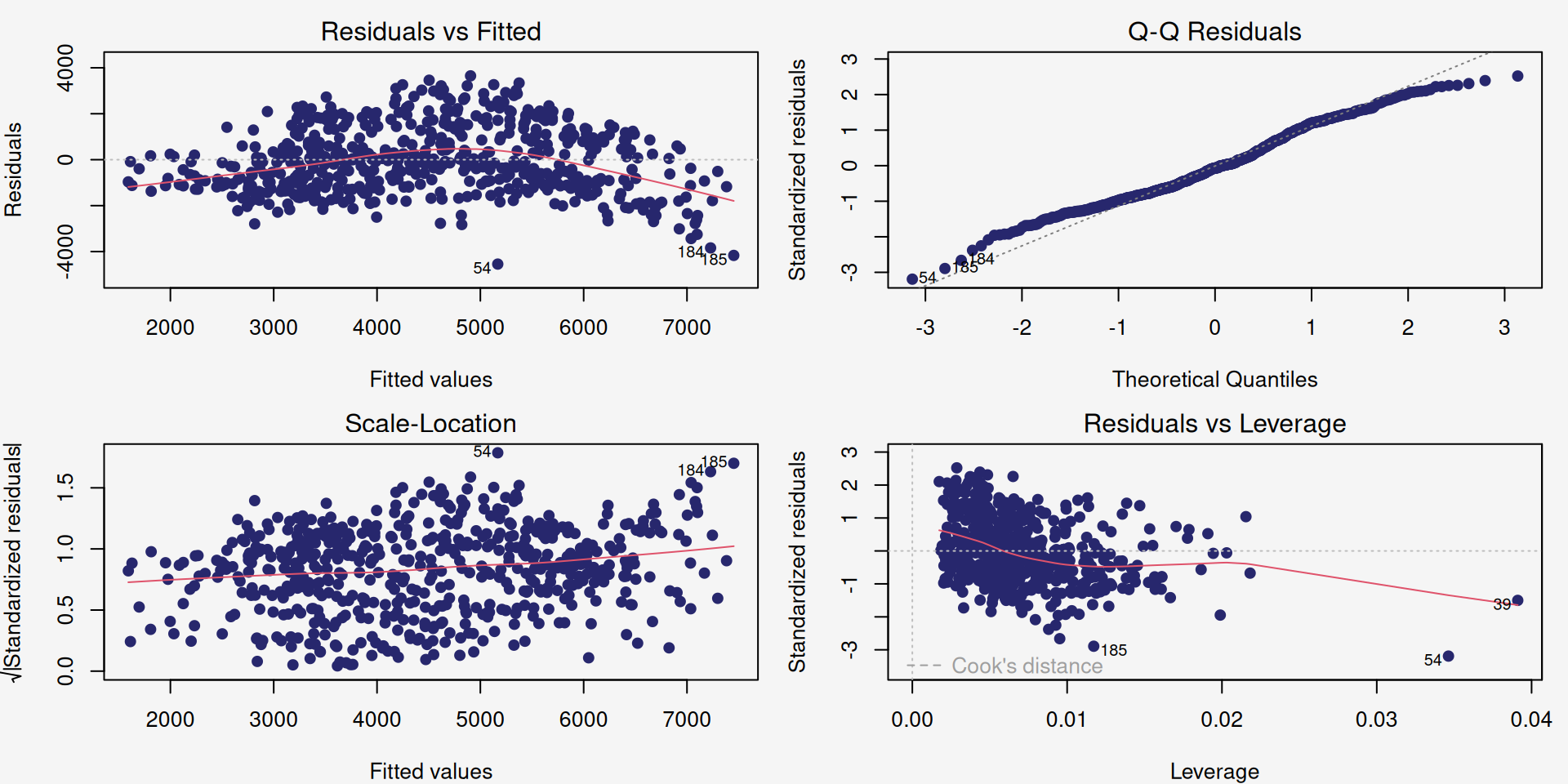
Conclusão do Mundo 1: O gráfico de resíduos vs. valores ajustados indica uma relação não linear entre os resíduos, violando a suposição de que os erros são independentes e aleatoriamente distribuídos. Podemos transofrmar a variável resposta ou usar um modelo diferente.

Mundo 2: PREDIÇÃO (A Hora da Verdade)

O modelo não é tão bom para explicar as relações entre as variáveis. Mas ele é bom para prever?

Vamos usar o modelo (treinado com bikes_treino) para fazer predições nos dados que ele nunca viu: bikes_teste.

# Usando o modelo para prever nos dados de TESTE
predicoes_teste <- predict(modelo, newdata = bikes_teste)

# Vamos juntar o valor real com o valor previsto (estimate)
resultados_teste <- bikes_teste |> 
  select(rentals) |> 
  mutate(.pred = predicoes_teste) # Adicionamos a coluna de predições

Mundo 2: As Métricas de Predição (RMSE e MAE)

Não olhamos mais para \(R^2\) ou p-valor. Agora, medimos o erro da predição.
Usamos o pacote yardstick (parte do tidymodels) para calcular as métricas no conjunto de teste.
- RMSE (Root Mean Squared Error): O erro médio, na mesma unidade (rentals). Ele penaliza erros grandes. Quanto menor, melhor.
- MAE (Mean Absolute Error): O erro médio absoluto. Mais fácil de interpretar. Quanto menor, melhor.

Mundo 2: As Métricas de Predição (RMSE e MAE)

# Calculando RMSE
rmse_val <- yardstick::rmse(resultados_teste, truth = rentals, estimate = .pred)
rmse_val

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 rmse    standard       1338.

# Calculando MAE
mae_val <- yardstick::mae(resultados_teste, truth = rentals, estimate = .pred)
mae_val

# A tibble: 1 × 3
  .metric .estimator .estimate
  <chr>   <chr>          <dbl>
1 mae     standard       1110.

Conclusão do Mundo 2: Em média, nosso modelo erra em ~1110 aluguéis (MAE) ao tentar prever os aluguéis de um dia novo. Considerando que os aluguéis variam de ~1000 a ~7500 (pelos gráficos), um erro de 1110 é substancial.

Mundo 2: Visualizando o Erro de Predição

Um gráfico de Valor Real vs. Valor Previsto é a melhor forma de ver a performance.

Se o modelo fosse perfeito, todos os pontos estariam dispostos em linha reta (Y = X).

ggplot(resultados_teste, aes(x = rentals, y = .pred)) +
  geom_point(color = "#27276d", alpha = 0.7, size = 2) +
  # A linha de predição perfeita (y=x)
  geom_abline(color = "red", linetype = "dashed", linewidth = 1.5) +
  labs(
    title = "Performance de Predição nos Dados de TESTE",
    x = "Valor Real (Aluguéis)",
    y = "Valor Previsto (Aluguéis)"
  ) +
  theme_minimal(base_size = 18) +
  # Força os eixos a terem a mesma escala para uma comparação justa
  coord_fixed()

Mundo 2: Visualizando o Erro de Predição

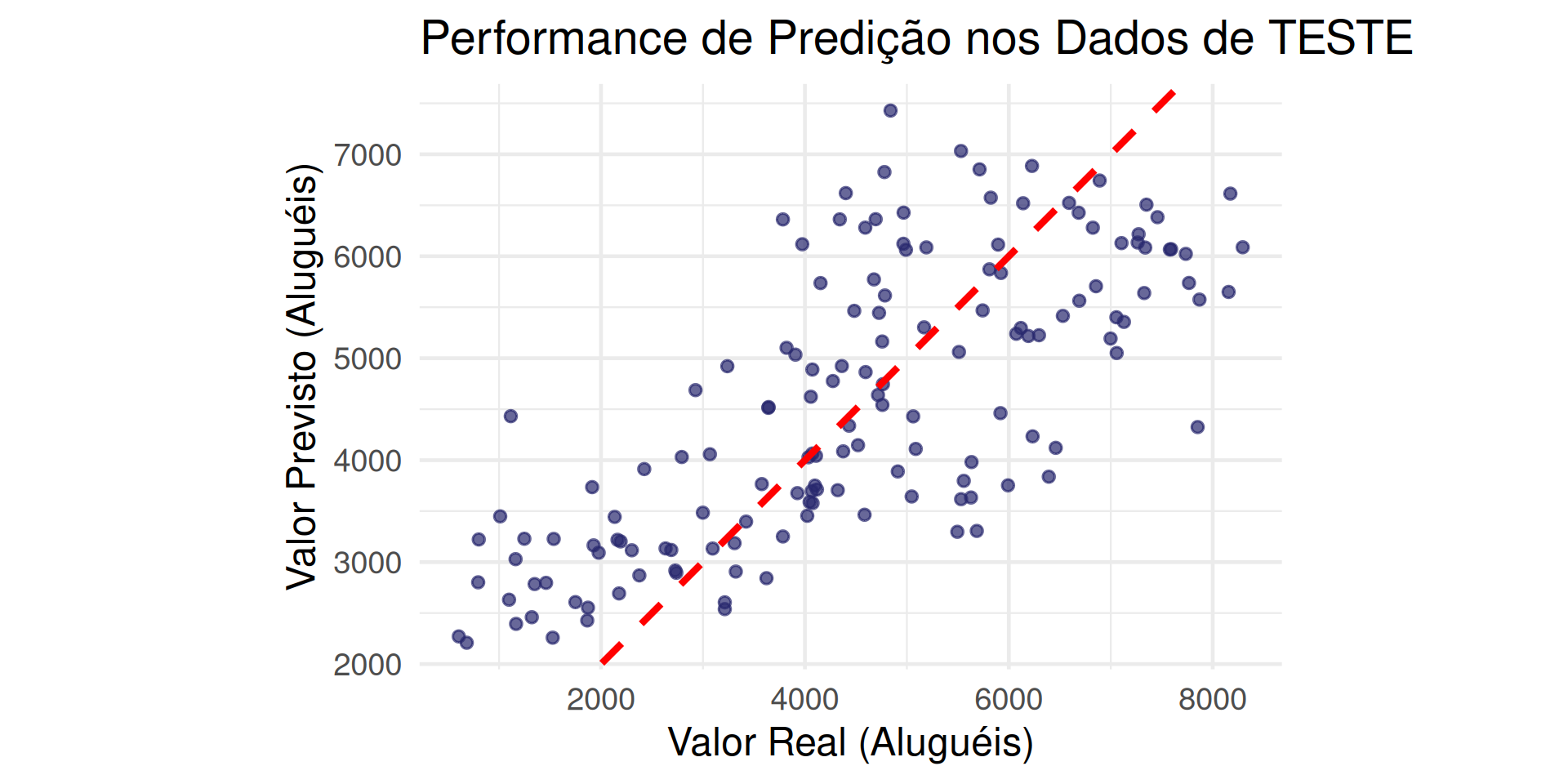
Insight: O modelo tende a superestimar dias com menos de 2000 alugueis e a subestimar dias com muitos aluguéis (pontos acima de 6000).

Modelos Mais Avançados

Quando o modelo linear falha, devemos tentar transformar a variaǘel resposta ou entar outros modelos, como GAMs (Modelos Aditivos Generalizados) ou Árvores de Regressão (e Random Forest).
No caso de modelos para predição, usamos diversos modelos diferentes e ficamos com aquele que apresentar menor RMSE/MAE nos dados de teste.

Inferência vs. Predição

A Regressão Linear pode servir a dois propósitos:

Característica	INFERÊNCIA	PREDIÇÃO
Objetivo	Explicar, Entender Relações	Prever, Generalizar
Métricas	\(R^2\), \(R^2\) Ajustado, p-valores, Teste F	RMSE, MAE, MAPE
Dados usados	Treino	Teste
Pergunta	“Meu modelo é válido e as variáveis são significativas?”	“Meu modelo é preciso em dados novos?”
Risco	Confundir \(R^2\) alto com boa predição.	Overfitting (se não usar o teste).

Um bom cientista de dados domina ambos os mundos.

Regressão Linear

Objetivo da Aula

Panorama Geral de Mineração de Dados

Problema: Aluguel de Bicicletas

Regra de Ouro da Aprendizagem Supervisionada

Solução: Partição Treino-Teste

Solução: Partição Treino-Teste

A Abordagem de “Dois Mundos”

Mundo 1: INFERÊNCIA (Explorando as Relações)

Mundo 1: INFERÊNCIA (Explorando as Relações)

Mundo 1: Ajustando o Modelo Linear Múltiplo

Mundo 1: Interpretando o summary()

Mundo 1: Interpretando o summary()

Mundo 1: Interpretando o summary()

Mundo 1: Diagnóstico (Validando as Suposições)

Mundo 1: Diagnóstico (Validando as Suposições)

Mundo 2: PREDIÇÃO (A Hora da Verdade)

Mundo 2: As Métricas de Predição (RMSE e MAE)

Mundo 2: As Métricas de Predição (RMSE e MAE)

Mundo 2: Visualizando o Erro de Predição

Mundo 2: Visualizando o Erro de Predição

Modelos Mais Avançados

Inferência vs. Predição

Agora vamos fazer no R…

Mundo 1: Interpretando o `summary()`

Mundo 1: Interpretando o `summary()`

Mundo 1: Interpretando o `summary()`