Regressão Logística

ESTAT0109 – Mineração de Dados em Estatística

Prof. Dr. Sadraque E. F. Lucena
sadraquelucena@academico.ufs.br
http://sadraquelucena.github.io/mineracao

Objetivo da Aula

Compreender por que a Regressão Linear falha em classificação e como a Função Sigmoide resolve isso limitando as probabilidades entre 0 e 1.
Aprender a ajustar um modelo de Regressão Logística para prever a probabilidade de eventos binários (Sim/Não, Fraude/Legal, 0/1).
Ler os coeficientes não apenas como números, mas como fatores de risco (Odds Ratio) que aumentam ou diminuem a chance do evento.
Superar a “ilusão da acurácia” aprendendo a usar Matriz de Confusão, Sensibilidade, Especificidade e Curva ROC/AUC para validar o modelo.

Regressão Logística: O Classificador

A regressão logística é a técnica fundamental para classificação binária.
Diferente da regressão linear (que prevê valores contínuos), aqui queremos estimar a probabilidade de um evento ocorrer.
Aplicações em Mineração de Dados:
- Churn: Prever se um cliente vai cancelar o serviço ($Y=1$) ou ficar ($Y=0$).
- Fraude: Identificar se uma transação é fraudulenta ou legítima.
- Medicina: Classificar um tumor como maligno ou benigno com base em exames.
- Crédito: Estimar o risco de inadimplência (default).

Formulação

Considere $y_i$ como nossa variável alvo (Target) binária: \[ \begin{cases} y_i = 1, & \text{ (evento de interesse: fraude, óbito, clique)}\\ y_i = 0, & \text{ (evento negativo)} \end{cases} \]
Temos um conjunto de features (variáveis explicativas) $\underset{\sim}{x} = x_1,x_2,\ldots,x_p$.
Objetivo da Predição: Não queremos apenas “0” ou “1”, mas sim a probabilidade ($\pi_i$) de pertencer à classe positiva: \[ P(y_i=1|~\underset{\sim}{x}) = \pi_i \]

Por que não usar Regressão Linear?

Tentar ajustar uma reta $\pi_i = \beta_0 + \beta_1 x$ gera dois problemas fatais para classificação:
1. Violação de Limites: Uma reta pode prever probabilidades absurdas, como $-0.2$ ou $1.5$. Probabilidade deve estar sempre entre $[0, 1]$.
2. Não-Linearidade: A transição de “não acontecer” para “acontecer” raramente é linear; geralmente é abrupta (como um “S”).

Precisamos de uma função que “esprema” as predições para dentro do intervalo $[0,1]$.

A Solução: Função Logística (Sigmoide)

Para garantir que a predição $\pi_i$ fique entre 0 e 1, usamos a Função Logística:

\[ \pi_i = \frac{1}{1 + e^{-(\beta_0 + \beta_1 x_{1i} + \cdots + \beta_{p}x_{pi})}} \]

Essa fórmula gera uma curva em formato de S (Sigmoide).
O termo dentro da exponencial, $\beta_0 + \beta_1 x + \dots$, é chamado de score ou preditor linear.
- Se o score for muito alto $\to \pi_i \approx 1$.
- Se o score for muito baixo (negativo) $\to \pi_i \approx 0$.
- Se o score for zero $\to \pi_i = 0.5$.

O “Logit” (Linearizando o problema)

Podemos reescrever a equação anterior para torná-la linear nos parâmetros. Isso facilita a estimativa:

\[ \underbrace{\log\left( \frac{\pi_i}{1-\pi_i} \right)}_{\text{Logit}} = \beta_0 + \beta_1 x_{1i} + \cdots + \beta_{p}x_{pi} \]

Logit: É o logaritmo da chance (log-odds).
Interpretação Visual:
- O lado direito é a nossa velha conhecida equação linear.
- O lado esquerdo é a transformação necessária para adequar a probabilidade ao mundo linear.

Estimando os Parâmetros (O “Fit”)

Como encontramos os melhores $\beta$?
Na regressão linear, usávamos Mínimos Quadrados (menor distância entre pontos e reta).
Na logística, usamos Máxima Verossimilhança (Maximum Likelihood Estimation - MLE).
- Intuição: O algoritmo busca os valores de $\beta$ que maximizam a probabilidade de observar os dados que realmente coletamos.
- Em Machine Learning, isso é equivalente a minimizar a função de custo Log-Loss (Entropia Cruzada).

Nota: Não usamos $R^2$ aqui. A qualidade do ajuste será medida pela capacidade de classificar corretamente (Acurácia, ROC, AUC).

Fazendo a Predição

Uma vez que o modelo “aprendeu” os $\beta$s, fazemos a predição em novos dados em dois passos:

Calcular o Score Linear: $\eta_i = \hat{\beta}_0 + \hat{\beta}_1 x_1 + \dots$
Converter para Probabilidade: $\hat{\pi}_i = \frac{exp(\eta_i)}{1+exp(\eta_i)}$

Exemplo Prático

Modelo ajustado para prever Inadimplência ($y=1$): \[ \text{logit}(\pi) = -10.65 + 0.0055 \times (\text{Saldo Devedor}) \]

Pergunta: Qual a probabilidade de calote para um saldo de $2.000?

Cálculo:

$\eta = -10.65 + 0.0055(2000) = -10.65 + 11 = 0.35$
$\pi = \frac{e^{0.35}}{1 + e^{0.35}} = \frac{1.419}{2.419} \approx 0.58$

Conclusão: Há 58% de probabilidade de inadimplência. O modelo classifica como “Mau Pagador” (se o corte for 0.5).

Interpretando os Coeficientes (Odds Ratio)

Em Machine Learning, muitas vezes focamos apenas na predição, mas entender os coeficientes ajuda a explicar o modelo (“Explainable AI”).
O $\beta$ nos diz como o logaritmo da chance muda. Para facilitar, usamos o Odds Ratio (OR) = $e^\beta$.
Regra de Bolso:
- OR > 1: A variável aumenta a chance do evento (Risco).
- OR < 1: A variável diminui a chance do evento (Proteção).
- OR = 1: A variável não afeta a predição.

Exemplo de Interpretação

Modelo de Risco de Crédito: \[ \text{logit} = -10.8 + \underbrace{0.0057}_{\beta_1} \text{Saldo} + \underbrace{0.0001}_{\beta_2} \text{Salário} - \underbrace{0.65}_{\beta_3} \text{Estudante (Sim)} \]

Saldo ($e^{0.0057} \approx 1.006$): A cada $1 dólar a mais de dívida, o risco aumenta ligeiramente (0.6%).
Estudante ($e^{-0.65} \approx 0.52$):
- O valor é menor que 1. Isso indica proteção.
- Ser estudante reduz a chance de inadimplência em cerca de 48% ($1 - 0.52$) comparado a não-estudantes, mantendo as outras variáveis constantes.

Da Probabilidade à Decisão (Threshold)

O modelo cospe uma probabilidade (ex: $0.7$, $0.2$, $0.55$).
Para tomar uma decisão (negar crédito, dar remédio), precisamos de um Ponto de Corte (Threshold) $c$ de forma que

\[ \begin{cases} \pi_i \geq c \Rightarrow \text{Classifica como 1 (Positivo)} \\ \pi_i < c \Rightarrow \text{Classifica como 0 (Negativo)} \end{cases} \]

Padrão: $c = 0.5$
Ajustável: Dependendo do problema, podemos subir ou descer a régua.

Avaliação: Matriz de Confusão

Comparação entre o Real e o Predito:

	Negativo Real (0)	Positivo Real (1)
Predito 0	Verdadeiro Negativo (VN)	Falso Negativo (FN) (Erro Tipo II)
Predito 1	Falso Positivo (FP) (Erro Tipo I)	Verdadeiro Positivo (VP)

Acurácia: De tudo que tentei prever, quanto acertei? \[\frac{VP + VN}{\text{Total}}\]
Cuidado: Acurácia engana em dados desbalanceados!

O Problema do Desbalanceamento

Imagine que usamos corte = 0.5 em dois modelos diferentes.

Cenário Real: Temos muito mais “Zeros” (Bons Pagadores) do que “Uns” (Maus Pagadores).

Se o modelo “chutar” que todo mundo é bom pagador (0):
- Ele terá altíssima acurácia (ex: 90%).
- Mas terá zero capacidade de detectar a fraude/inadimplência (Sensibilidade = 0).

Em Data Mining, raramente olhamos apenas para Acurácia. Precisamos olhar para Sensibilidade e Precisão.

Curva ROC e AUC

Como escolher o melhor ponto de corte $c$? Não queremos testar um por um manualmente.
A Curva ROC plota a performance do modelo para TODOS os pontos de corte possíveis.
Eixos:
- Y: Sensibilidade (Taxa de VP): Capacidade de detectar o evento.
- X: 1 - Especificidade (Taxa de FP): Taxa de alarme falso.

Curva ROC e AUC

A melhor curva é a que “abraça” o canto superior esquerdo.

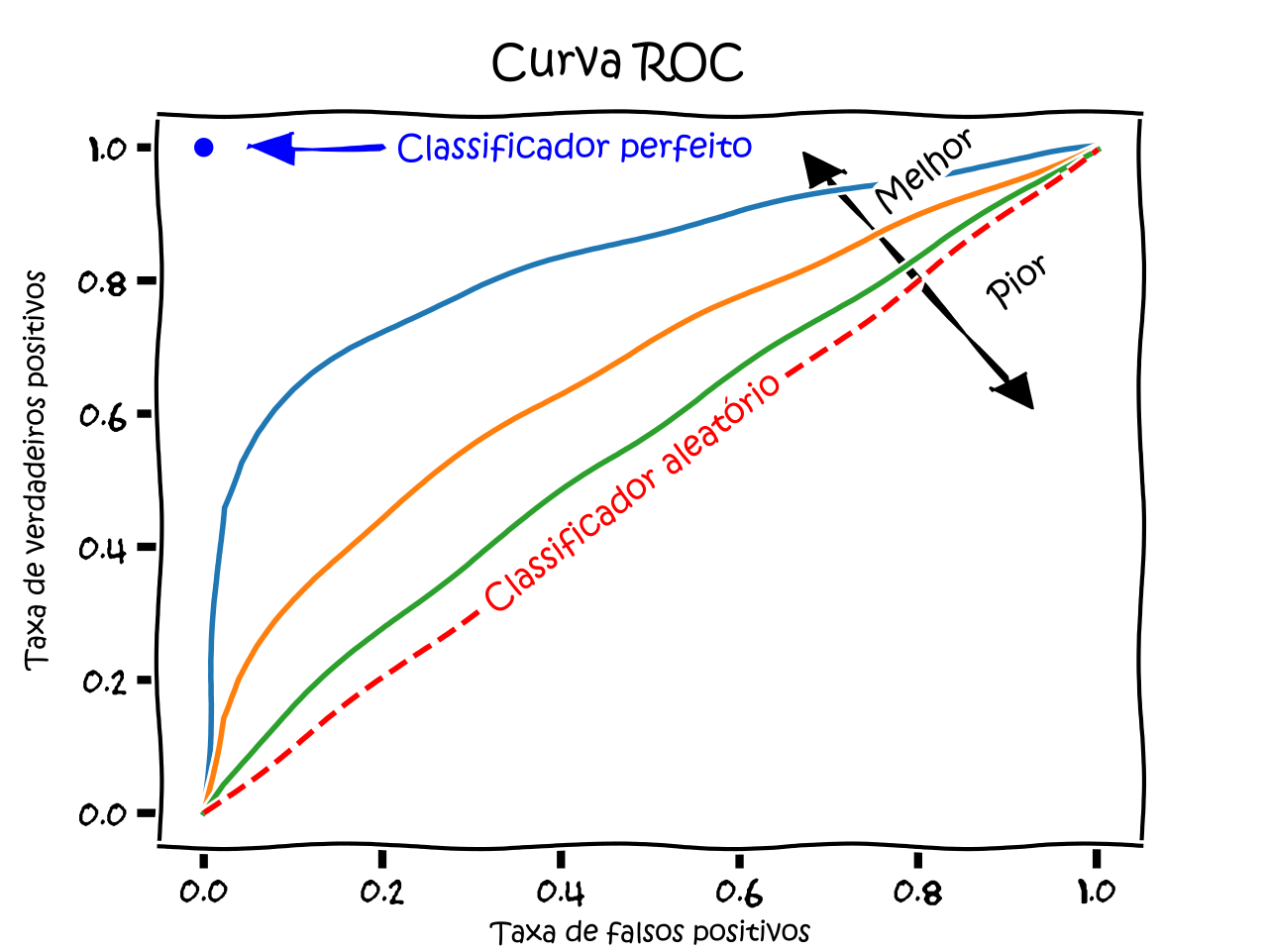
FONTE: Wikipedia.

Interpretando a AUC (Area Under Curve)

A área abaixo dessa curva resume a qualidade do modelo em um único número.

Valor AUC	Interpretação
0.5	Aleatório (Igual a jogar moeda)
0.7 - 0.8	Aceitável
0.8 - 0.9	Excelente
> 0.9	Suspeite de vazamento de dados (Overfitting)

Objetivo: Maximizar a AUC.

Validação Cruzada (A Regra de Ouro)

Nunca avaliamos o modelo nos mesmos dados usados para criar os $\beta$. Isso seria “decorar a prova”.

Hold-out: Separar 70% Treino / 30% Teste.
K-Fold Cross Validation:
- Divide os dados em $k$ partes (ex: 10).
- Treina em 9, testa em 1.
- Repete 10 vezes e tira a média.

Só confiamos na métrica (Acurácia/AUC) obtida na base de TESTE.

Regressão Logística

Objetivo da Aula

Regressão Logística: O Classificador

Formulação

Por que não usar Regressão Linear?

A Solução: Função Logística (Sigmoide)

O “Logit” (Linearizando o problema)

Estimando os Parâmetros (O “Fit”)

Fazendo a Predição

Exemplo Prático

Interpretando os Coeficientes (Odds Ratio)

Exemplo de Interpretação

Da Probabilidade à Decisão (Threshold)

Avaliação: Matriz de Confusão

O Problema do Desbalanceamento

Curva ROC e AUC

Curva ROC e AUC

Interpretando a AUC (Area Under Curve)

Validação Cruzada (A Regra de Ouro)

Agora vamos fazer no R…