K-Nearest Neighbors (k-NN)

ESTAT0109 – Mineração de Dados em Estatística

Prof. Dr. Sadraque E. F. Lucena
sadraquelucena@academico.ufs.br
http://sadraquelucena.github.io/mineracao

Objetivo da Aula

• Compreender a intuição e o funcionamento matemático do algoritmo k-NN para tarefas de Classificação e Regressão.
• Aplicar técnicas essenciais de pré-processamento, com ênfase na normalização de dados numéricos e codificação de variáveis categóricas.
• Calcular manualmente a distância euclidiana para determinar a similaridade entre instâncias.
• Analisar o impacto da escolha do hiperparâmetro \(k\) no tradeoff entre viés e variância (overfitting vs underfitting).
• Avaliar as vantagens e limitações do paradigma de “aprendizado preguiçoso” (lazy learning) em comparação a modelos ansiosos.

Classificadores de vizinhos mais próximos (nearest neighbors)

• São classificadores que atribuem rótulos a instâncias não rotuladas a partir da similaridade com exemplos rotulados.
• Esses classificadores buscam replicar a capacidade humana de extrair conclusões sobre situações atuais a partir de experiências passadas.
• Exemplos de aplicações bem sucedidas:
  • Visão computacional: reconhecimento de caracteres e reconhecimento facial em imagens estáticas e vídeos;
  • Sistemas de recomendação que preveem se uma pessoa irá gostar de um filme ou música;
  • Identificação de padrões em dados genéticos para detectar proteínas ou doenças específicas.

O algoritmo k-NN

• O algoritmo k-NN utiliza informações sobre os \(k\) vizinhos mais próximos de um exemplo para classificar exemplos não rotulados.

• A letra \(k\) representa o número de vizinhos mais próximos que serão usados para a classificação de uma instância sem rótulo.

  • Definido \(k\), o algoritmo usa um conjunto de dados de treinamento classificados em várias categorias.
  • Para cada instância não rotulada, o k-NN identifica as \(k\) instâncias mais similares nos dados de treinamento.
  • À instância sem rótulo é atribuída a classe da maioria dos \(k\) vizinhos mais próximos.

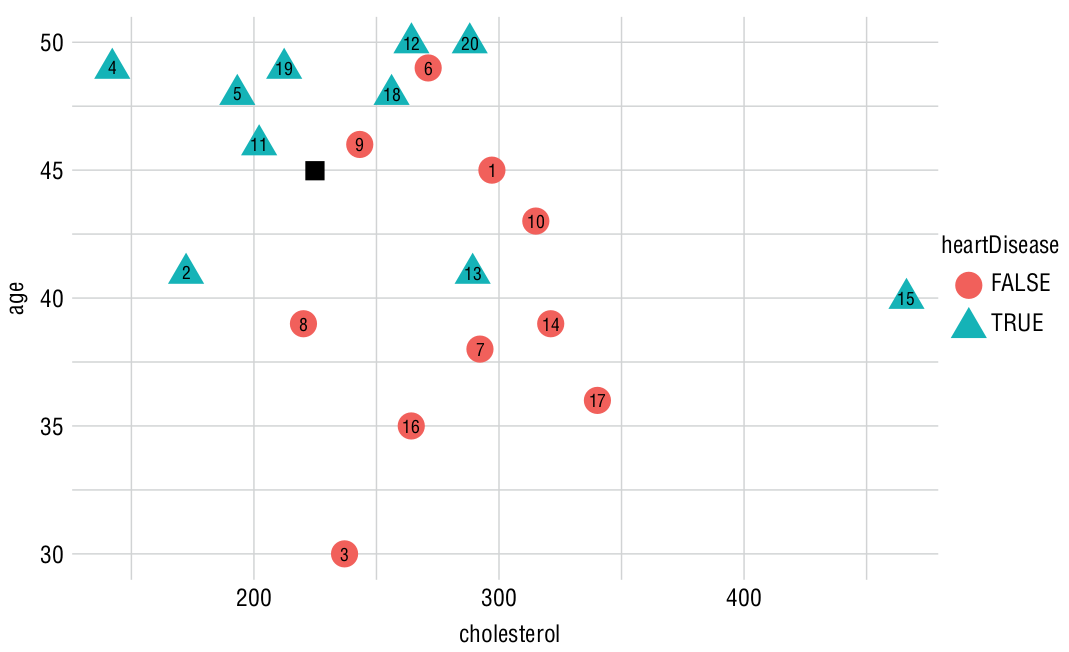
FONTE: NWANGANGA, Fred; CHAPPLE, Mike. Practical machine learning in R. John Wiley & Sons, 2020.

Vantagens e desvantagens

Vantagens

• Simples e efetivo.
• Não faz suposições sobre a distribuição dos dados (não paramétrico).
• Fase de treinamento rápida (apenas armazena os dados).

Desvantagens

• Não produz um modelo explícito, limitando a interpretabilidade de como as características afetam a classe.
• Requer a seleção de um \(k\) apropriado.
• Fase de classificação lenta (custosa computacionalmente).
• Características nominais e dados ausentes exigem processamento adicional cuidadoso.

Encontrando os vizinhos mais próximos

• Para encontrar os vizinhos mais próximos de uma instância é preciso calcular a distância entre as instâncias.
• Tradicionalmente, o algoritmo k-NN usa a distância euclidiana:
  • Sejam \(p\) e \(q\) duas instâncias com \(n\) atributos. Então a distância euclidiana entre \(p\) e \(q\) é dada por \[ dist(p,q) = \sqrt{(p_1-q_1)^2 +(p_2-q_2)^2 + \cdots + (p_n-q_n)^2} \] em que \(p_i\) e \(q_i\), \(i=1,\ldots,n\), representam os atributos associados às instâncias \(p\) e \(q\), respectivamente.
• Outras distâncias que podem ser usadas: distância de Hamming, distância de Manhattan (ou L1), distância Minkowski e distância de Mahalanobis.

Preparando os dados

• Observação: antes do cálculo da distância euclidiana devemos normalizar os atributos, pois atributos com valores mais elevados tendem a ter um impacto desproporcional no cálculo de distância.
• Para o k-NN podemos usar a normalização min-max: \[ x_{novo} = \frac{x - min(X)}{max(X)-min(X)} \]
• ou a transformação z-score: \[ x_{novo} = \frac{x - média(X)}{DesvPad(X)}. \]

Preparando os dados (Variáveis Categóricas)

• Se o atributo é do tipo nominal, devemos transformá-lo.
• Atenção: Embora em regressão usemos \(n-1\) dummies, em algoritmos de distância (k-NN) é comum usar One-Hot Encoding (criar \(n\) variáveis) para manter a equidistância entre categorias.
• Exemplo: se o atributo temperatura possui as categorias quente, médio e frio:

\[ quente = \begin{cases} 1 & \text{se } x = \text{ quente}\\ 0 & \text{caso contrário} \end{cases} \] \[ frio = \begin{cases} 1 & \text{se } x = \text{ frio}\\ 0 & \text{caso contrário} \end{cases} \]

\[ médio = \begin{cases} 1 & \text{se } x = \text{ médio}\\ 0 & \text{caso contrário} \end{cases} \]

• Como a dummy possui apenas os valores 0 e 1, os valores caem na mesma escala da transformação min-max.

Exemplo

Considere os dados de treinamento abaixo. Calcule a distância euclidiana para um novo paciente com 45 anos e colesterol de 225 (após normalizar).

Paciente	Idade	Colesterol	Doença
1	45	297	F
2	41	172	V
3	46	202	V
4	48	193	V
5	46	243	F

Paciente	Idade	Colesterol	Doença
6	48	256	V
7	49	212	V
8	41	289	V
9	49	271	F
10	43	315	F

• Atividade: Ordene os dados de treino da menor distância para a maior distância do novo paciente e classifique usando \(k=3\).

Determinando \(k\) apropriado

• A decisão de quantos vizinhos usar determina a generalização do modelo (Tradeoff Viés-Variância).
  • \(k\) pequeno: Baixo viés, alta variância. O modelo é sensível a ruídos (Overfitting).
  • \(k\) grande: Alto viés, baixa variância. O modelo é muito simples e ignora padrões locais (Underfitting).
• O valor escolhido para \(k\) em classificação binária deve ser preferencialmente ímpar para evitar empates.
• Uma forma de determinar \(k\) é testar diversos valores com os dados de validação e escolher aquele com menor erro.

Por que o algoritmo k-NN é preguiçoso?

• Algoritmos de classificação baseados em métodos de vizinho mais próximo são considerados algoritmos de aprendizado preguiçoso (lazy learning).
• Um aprendiz preguiçoso não está realmente “aprendendo” um modelo matemático durante o treino; ele apenas armazena os dados.
• O processamento real acontece apenas na hora da classificação (inferência).
• O aprendizado preguiçoso também é conhecido como aprendizado baseado em instâncias ou aprendizado por repetição.

E a Regressão k-NN?

• Em problemas de regressão, a estimativa é numérica. Pode-se usar a média simples ou a média ponderada (preferível).
• A média ponderada pelo inverso da distância dá mais importância aos vizinhos muito próximos: \[ \widehat{y}_{nova} = \frac{\sum_{i=1}^k w_i \cdot y_i}{\sum_{i=1}^k w_i} \] em que:
  • \(y_i\) é o valor da variável resposta do vizinho \(i\);
  • \(w_i = \frac{1}{distancia(x_{novo}, x_i)}\) é o peso.

Escolha de \(k\) na Regressão k-NN

• O valor de \(k\) é escolhido como aquele que produz menor erro nos dados de validação. Métricas comuns:

  • Erro médio absoluto (MAE):
    \[MAE(y,\widehat{y}) = \frac{1}{n}\sum\limits_{i=1}^n|y_i-\widehat{y}_i|\]

  • Erro quadrático médio (MSE): \[MSE(y,\widehat{y}) = \frac{1}{n}\sum\limits_{i=1}^n (y_i-\widehat{y}_i)^2\]

Escolha de \(k\) na Regressão k-NN

• Raiz do erro quadrático médio (RMSE): \[RMSE(y,\widehat{y}) = \sqrt{\frac{1}{n}\sum\limits_{i=1}^n (y_i-\widehat{y}_i)^2}\]

Agora vamos fazer no R…