Support Vector Machines (SVM)
ESTAT0109 – Mineração de Dados em Estatística
Prof. Dr. Sadraque E. F. Lucena
sadraquelucena@academico.ufs.br
http://sadraquelucena.github.io/mineracao
Objetivo da Aula
- Compreender a maximização da margem, o problema dual e o truque de kernel.
Ideia central do SVM
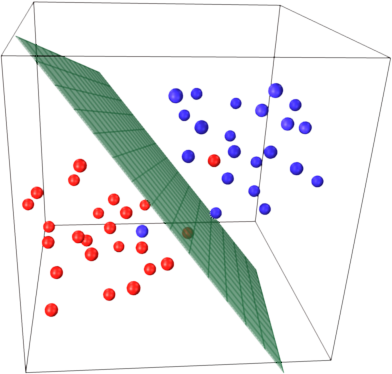
- Imagine um conjunto de pontos espalhados em um espaço, em que cada ponto representa um dado e pertence a uma determinada classe. O objetivo do algoritmo de Support Vector Machine (SVM) é encontrar uma forma de separar esses pontos de acordo com suas classes.
- Para isso, a SVM procura uma linha (em duas dimensões), um plano (em três dimensões) ou, de forma mais geral, um hiperplano, que divida o espaço de maneira a separar os pontos de classes diferentes. No entanto, não basta apenas separar: a SVM busca o hiperplano ótimo, isto é, aquele que maximiza a distância entre a fronteira de separação e os pontos mais próximos de cada classe.
- Esses pontos mais próximos do hiperplano são chamados de vetores de suporte e são fundamentais para definir a posição da fronteira de decisão. Ao maximizar essa margem de separação, a SVM tende a produzir modelos com melhor capacidade de generalização, ou seja, mais eficientes para classificar corretamente novos dados que não foram utilizados no treinamento.
Fonte: https://umeshchandra.in/2024/04/19/understanding-support-vector-machines-svm/
Exemplos de Aplicações de SVM
- As SVMs podem ser usadas para classificação e para previsão numérica.
- Exemplos:
- Classificação de dados de expressão gênica para identificar câncer ou outras doenças genéticas;
- Identificação do idioma usado em um documento ou a organização de documentos por assunto;
- Detecção de eventos raros, como falhas em motores de combustão, violações de segurança ou terremotos.
- As SVMs têm sido tradicionalmente aplicadas em classificação binária. Portanto, focaremos apenas em classificadores SVM. É importante saber que os mesmos princípios se aplicam à adaptação das SVMs para previsão numérica (regressão).
Conceitos Chave de SVMs
Hiperplano: fronteira de decisão que separa os dados em classes diferentes. Em um problema de classificação binária, o hiperplano é definido como a linha que maximiza a margem entre as duas classes.
Vetores de Suporte: pontos de dados mais próximos do hiperplano. São usados para definir a margem e ajustar o hiperplano de modo a alcançar um melhor desempenho de classificação.
Truque do Kernel (Kernel Trick): As SVMs podem lidar de forma eficiente com tarefas de classificação não linear por meio do uso do truque do kernel. Essa técnica consiste em mapear o espaço original de atributos para um espaço de maior dimensão, no qual os dados se tornam linearmente separáveis. Funções de kernel comuns incluem os kernels linear, polinomial, de função de base radial (RBF) e sigmoide.
Classificação com Hiperplanos
- Quando os elementos podem ser divididos por uma linha reta ou por uma superfície plana, diz-se que eles são linearmente separáveis, mas elas também podem ser estendidas para problemas em que os dados não são linearmente separáveis.
- Existe mais de uma escolha possível de linha divisória entre os grupos de círculos e quadrados. Como o algoritmo decide qual delas escolher?
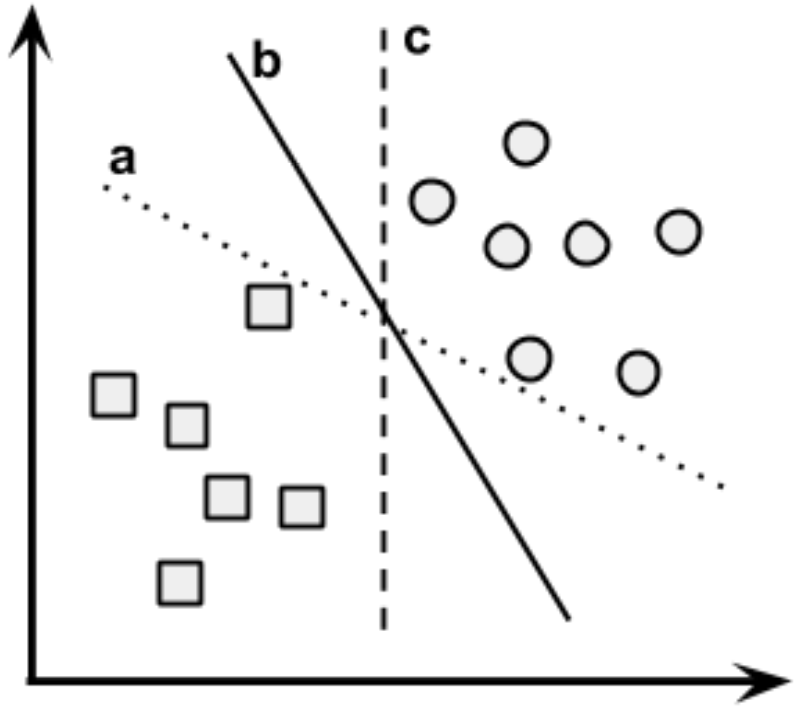
Fonte: Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
Encontrando a Margem Máxima
- Na imagem anterior, vários linhas separam corretamente os dados.
- No entanto, a linha (hiperplano) que cria a maior separação possível entre as classes (maximiza a margem) tende a generalizar melhor para novos dados.
- Isso ocorre porque pequenas variações nos pontos próximos à fronteira podem causar erros de classificação se a margem for pequena.
- Para determinar o Hiperplano de Margem Máxima (Maximum Margin Hyperplane – MMH), são usados os vetores de suporte (pontos mais próximos da fronteira, do MMH).
- A identificação dos vetores de suporte envolve geometria vetorial e matemática avançada, mas os conceitos fundamentais são intuitivos.
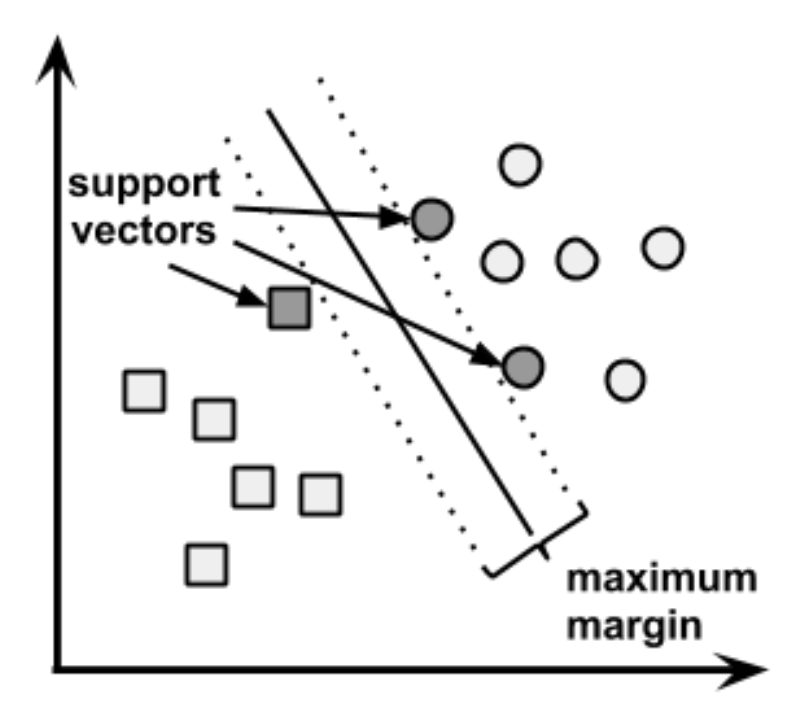
Fonte: Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
O Caso de Dados Linearmente Separáveis
- Nesse caso, o Hiperplano de Margem Máxima (MMH) fica o mais distante possível das fronteiras externas dos dois grupos de dados.
- Essas fronteiras externas são conhecidas como o envoltório convexo (convex hull).
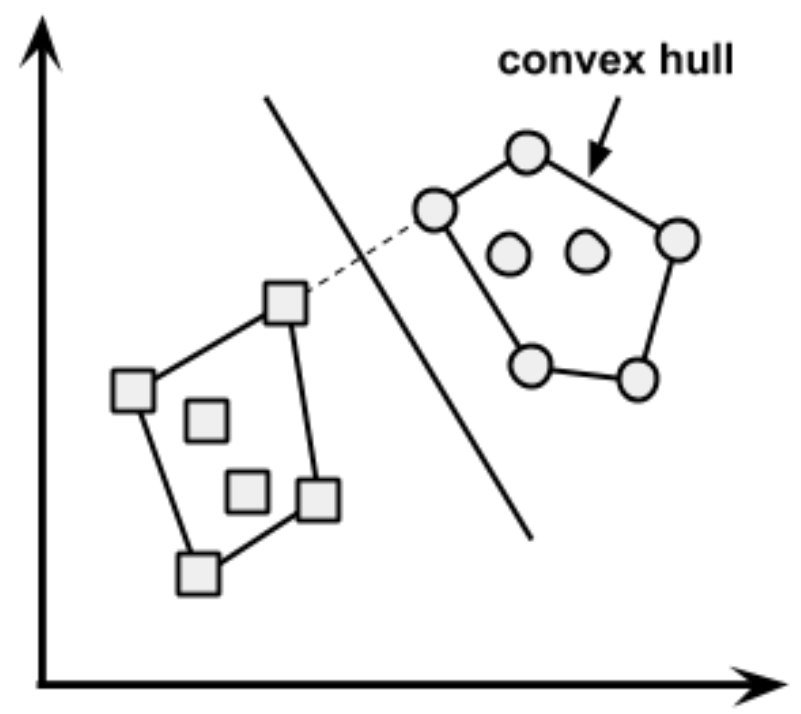
Fonte: Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
- O MMH corresponde à reta (ou plano) que fica exatamente no meio da menor distância entre os dois conjuntos, sendo perpendicular a essa reta. Ela é determinada por algoritmos numéricos que resolvem um problema de otimização quadrática.
O Caso de Dados Linearmente Separáveis
- Um hiperplano em espaço n-dimensional é definido pela equação \[ \vec{w} \cdot \vec{x} + b = 0 \]
- O objetivo é encontrar dois hiperplanos paralelos, um para cada classe, garantindo separação correta dos dados.
- A distância entre esses hiperplanos é inversamente proporcional à norma de \(w\).
- Maximizar a margem equivale a minimizar \(||\vec{w}||\).
- O problema é formulado como uma otimização com restrições que garantem a classificação correta de todos os pontos.
- Apesar da matemática envolvida, algoritmos especializados resolvem esse problema de forma eficiente, mesmo em bases grandes.
O Caso de Dados Não Linearmente Separáveis
- Nesse caso, a SVM utiliza uma margem suave (soft margin).
- A margem suave permite que alguns pontos sejam classificados incorretamente.
- Isso é feito por meio das variáveis de folga (ξ), que medem o quanto cada ponto viola a margem.
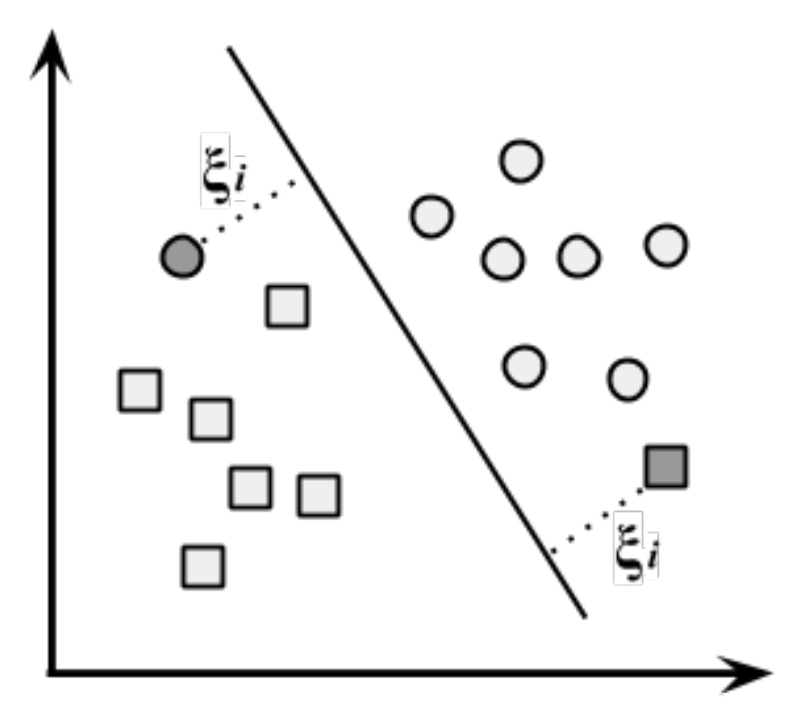
Fonte: Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
O Caso de Dados Não Linearmente Separáveis
- Um parâmetro de custo C penaliza pontos que violam as margens.
- O objetivo deixa de ser apenas maximizar a margem e passa a ser equilibrar margem larga e erro de classificação.
- Valores altos de C forçam o modelo a errar menos, mesmo que a margem fique menor.
- Valores baixos de C permitem mais erros, mas favorecem uma margem maior.
- Escolher corretamente C é essencial para obter um modelo que generalize bem.
Uso de Kernels para Espaços Não Lineares
- Uma alternativa ao uso da margem suave é aplicar o truque do kernel.
- O truque do kernel mapeia os dados para um espaço de maior dimensão, onde uma separação linear se torna possível.
- Esse mapeamento cria novas características implícitas, baseadas em relações matemáticas entre os atributos originais.
- Um padrão não linear no espaço original pode se tornar linearmente separável em um espaço transformado.
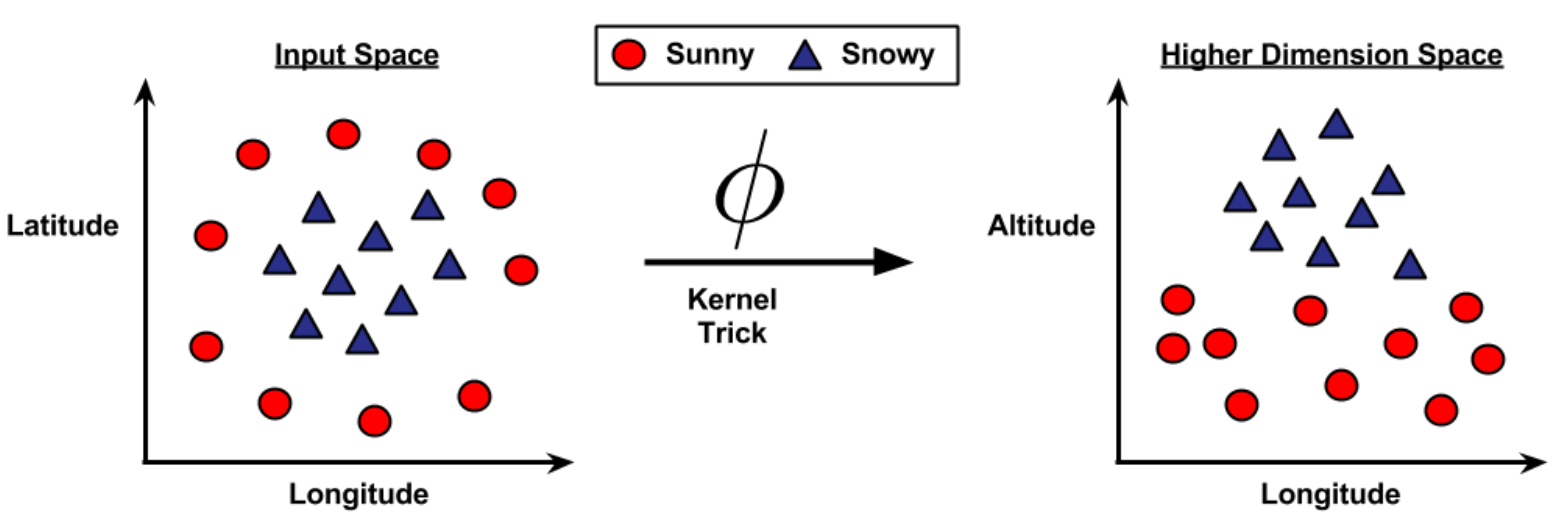
Fonte: Brett Lantz. Machine Learning with R. Packt Publishing, 2013.
Uso de Kernels para Espaços Não Lineares
- SVMs com kernels não lineares:
- São muito poderosas
- Lidam bem com ruído
- Geralmente generalizam bem
- Mas produzem modelos difíceis de interpretar
Uso de Kernels para Espaços Não Lineares
- Principais kernels:
- Linear: sem transformação
- Polinomial: adiciona relações não lineares simples
- Sigmoide: semelhante a redes neurais
- RBF Gaussiano: flexível, robusto e frequentemente usado como padrão inicial
- Não existe uma regra fixa para escolher o kernel ideal:
- depende dos dados
- depende do problema
- normalmente envolve validação e tentativa e erro
Agora vamos fazer no R…
